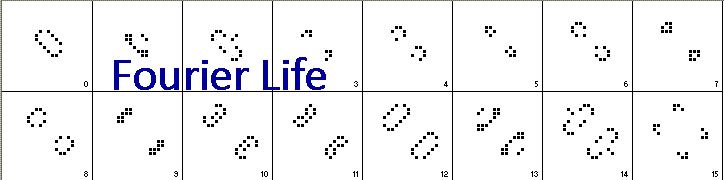
Fourier Life is a system of cellular automata which spontaneously forms self-replicating structures. The picture above has the first system I found and shows 16 iterations of the system (each square with dots in it is a small portion of the cellular automata grid). Note that after 12 iterations, the original structure has replicated itself, although now each copy is rotated from the original. At each iteration (or generation), a filled cell either survives or dies and an empty cell can either remain empty or have a cell born into it. In the example above, the fate of each cell depends on how many neighbors (filled cells) it has surrounding it (up to 8).
If you click on the Run button (under the grid of cells at the top of the page) with System A and Rule 1 selected, you can see these structures appear out of a random field of cells, begin dividing in two, and then take over the entire cellular automata world.
This web site shows the more interesting self-replicating systems I've found and describes how I found them. The key to detecting self-replicating systems is to use a Fourier Transform on the population graphs. As a result, I have named these systems Fourier Life.

No comments:
Post a Comment