Cellular Automata and the Origin of Life
Fourier Life deals with cellular automata, of which the most famous example is Conway's Game of Life.
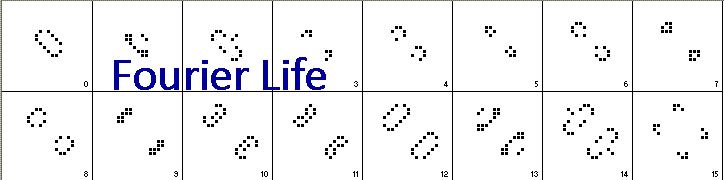
After discovering the first system, I wanted to find more self-replicating systems which would spontaneously appear out of a random field of cells. The visual analogy to the first life forms spontaneously coming into existence from the primordial soup is striking. See my Implications post for more speculation on this analogy.
Others have discovered or invented self-replicating systems in cellular automata, a collection of which is demonstrated on this nice web site from the New England Complex Systems Institute. The work described on this web site is complimentary to this earlier work and differs in three important ways:
- The self-replicating systems are emergent from a random population of cells--they were not designed.
- The self-replicating creatures (for lack of a better term) appear in systems simpler than the previous ones (two- and three-state systems rather than six- to nine-state systems)
- An algorithm using Fourier Transform was developed to find these emergent self-replicating systems
DISCLAIMER
I'm just a computer hobbyist, not a scientist in the field of artificial life (my day job is an organic chemist trying to discover new medicines). As a result, I am not up-to-date on all the relevant research. If you know of such research, please add a comment below.
No comments:
Post a Comment