Implications for the Origin of Life

Finding simple systems which spontaneously generate self-replicating groups of cells from a random soup seems to have implications for the Origin of Life on Earth. This post explores those implications.

Theories on the Origin of Life

Wikipedia has a good summary on abiogenesis, or the Origin of Life, and talkorigins.org also has a good summary. One of the prevalent theories is the RNA World where the first self-replicating forms were RNA molecules that could catalyze the formation of more copies of themselves. This idea is conceptually simple, but it would be extremely rare that one of these molecules could form spontaneously (fortunately, life had millions--and perhaps billions--of years to originate).

But what if the first cells had a collection of simpler molecules that in combination could replicate themselves. This set of molecules is known as an Autocatalytic Set. And this is how modern cells replicate themselves, although the current system contains roughly a million molecules and includes DNA as the library from which all other molecules are made. Even a simpler autocatalytic set of a few dozen molecules would necessarily involve a complex process with many interactions. Aren't the chances of finding an autocatalytic set of simpler molecules just as unlikely as finding a self-replicating RNA molecule? Perhaps not! The emergent self-replicating systems presented on this website may provide support for the Autocatalytic-Set hypothesis.

Cellular Automata and Autocatalytic Sets

Consider this analogy:

• Each cell (either filled for empty) in the grid is a molecule
• Each unique cell state (empty/filled & number of neighbors) corresponds to a different type of molecule (even though they are represented by only two colors)
• Each iteration in the cellular automata corresponds to the molecules doing a reaction whereby they can change into other molecules (i.e. change state)

When we run one of the cellular automata systems with emergent self-replication, a pattern of cells ends up replicating itself, although not every type of cell is present at all times. This corresponds to a set of molecules replicating itself, even though all types of molecules are not present at the same time.

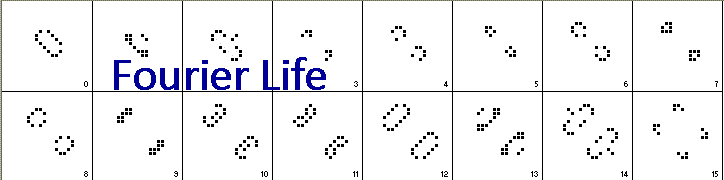
Let's consider an example. At iteration 3 below (the fourth frame), there are two patterns each with the following types of filled cells (n=neighbors): 1x1n, 2x2n, 1x3n and the following empty cells (excluding ones with 0 neighbors): 8x1n, 6x2n, 1x4n. But at iteration 4, there are two patterns with these filled cells: 1x0n, 2x1n, 3x2n and these empty cells: 12x1n, 9x2n, 2x3n, 1x4n.  The set of cell types has changed dramatically in a seemingly non-productive way. However, the cell types keep changing until we get to iteration 15 where the group of cells at iteration 3 has replicated itself! Thus, the exact number of the different cell types at iteration 3 had doubled (at the expense of the empty 0-neighbor cells), and this process continues with each replication period. Throughout the process, the "autocatalytic set" of cell types replicates itself, but in a messy process involving many intermediate steps, and it is difficult to see the process when viewed at the cell-type level. This is very similar to what we see with molecules in living cells today.

More than a hundred different emergent self-replicating rule-sets have been found in simple cellular automata systems using the Fourier Transform method. If the analogy above is correct, the soup of actual prebiotic molecules may also have many possible combinations which create autocatalytic sets.  Perhaps the Fourier Transform method can be applied to finding such sets in computer simulations.

My Favorite Theory on the Origin of Life

I like the paper by Hordijk, Hein and Steel entitled Autocatalytic Sets and the Origin of Life. They present a convincing argument that life may have started with autocatalytic sets. They also point out that if the set was contained inside a liposome which would allow food substrates to enter, the first cell could have been born.

I'll add to the theory above that if the autocatalytic set also included the machinery to make the liposome lipids, the whole system could replicate itself. Perhaps the primordial soup contained catalytic molecules which could carry out various catalytic reactions, including the ones necessary to extend aliphatic carbon chains to make lipids. Once the lipid concentrations are high enough (either through synthesis or concentration by evaporation), liposomes would form with random combinations of molecules trapped inside. If just one of these new lipsomes contained an autocatalytic set--including the ability to make more lipid molecules--the cell would continue to grow. New lipid molecules would become integrated into the liposome and when it became big enough, it would automatically divide. Each new liposome would (in most cases) contain the autocatalytic set of molecules and the process would start again. If this is indeed the process which occurred, this would then be the moment when life began.

Cellular Automata Systems

This post explains the cellular automata systems I've explored (each can be selected from the Cellular Automata System dropdown box above). All but the simplest system explored have produced self-replicating creatures which appear spontaneously from a random field of cells.

System	# of Rules	Emergent Self-Replicators
A. 2-State: Alternating Rules	232	yes
B. 2-State: Edge & Corner Combinations	248	yes
C. 3-State: Sum of All Edge States	324 (~238)	yes
D. 2-State: From Pattern (Conway-Like)	216	no (yes from pattern)

A. 2-State: Alternating Rules

This was the system in which the first emergent self-replicator was found (Sytem A, Rule 1). The system uses the Moore neighborhood and simply counts the total number of neighbors. However, unlike Conway's Life which uses the same rules for every iteration, my system alternates between two different rules. I found many self-replicating rules, but gave up on this system when I realized it isn't a local cellular automata, i.e. each cell needs not only the number of neighbors but also which generation the whole world is on.

B. 2-State: Edge & Corner Combinations

After abandoning the "2-State: Alternating Rules" system, I looked extensively in the 2-State, Moore neighborhood with just one rule for every iteration but didn't find anything. I thought having more possible rules might help. I decided to count the edge (E) and corner (C) neighbors separately and treat each combination of edge and corner neighbors as a Born/Survive rule. This new system had many more possible rules to explore (2^48 vs. 2^16), and I did find emergent self-replicators in it!

Below is the rule code for the Fourth of July rule (System B, Rule 1). The code is shown both as a written list of Born/Survive states and in a graphical view I created in my original Visual Basic 6 program.  The first entry (Rule-Born (E|C): 0|2) means that a cell is born into an empty cell if that cell has a combination of 0 edge neighbors and 2 corner neighbors.

Rule-Born (E|C): 0|2, 0|3, 1|4, 2|0, 2|3, 2|4, 3|2, 3|4, 4|0, 4|3, 4|4

Rule-Survive (E|C): 0|1, 1|2, 1|3, 1|4, 2|0, 2|4, 3|0, 3|2, 3|3, 4|4

C. 3-State: Sum of All Edge States

Once I had found self-replicating rules in the 2-State system, I was interested in exploring other systems.  The simplest 3-state system is to simply take the sum of the states (0, 1 or 2) of the edge neighbors (the von Neumann neighborhood). The range of values for any cell with at least one neighbor is 1 to 8 (the maximum has all four edge neighbors in state 2).

Below is the rule code for Game of Jacks (System C, Rule 2), both written out and in the visual representation from my Visual Basic 6 program. The 'N' refers to the neighbor sum and 'S' refers to the state that cell will be changed into (either 1 or 2 because state 0 is the empty cell). For example, the first rule (Rule-Born (N|S): 1|2) means that a cell will be born if the sum of neighbors is 1 and that cell will be born as state = 2. The last rule (Rule-State2 (N|S): 8|2) means that if a cell currently in state 2 has a neighbor sum of 8 it will be set to state 2 in the next iteration (i.e. stay as state 2).

Rule-Born (N|S): 1|2

Rule-State1 (N|S): 1|1, 3|1, 4|2, 6|1, 8|2

Rule-State2 (N|S): 1|1, 3|1, 4|1, 8|2

D. 2-State: From Pattern (Conway-Like)

Self-replicators have been described previously for simple Conway-Like systems by D. Eppstein on his Cellular Automata: Replicators page, but none emerge spontaneously from a small, random field of cells (or if they do, it is quite rare).  I found most of the self-replicators described by Eppstein by starting from a small group of cells, iterating for 512 generations, and then applying the Fourier Transform method to detect self-replicators.  So far, I have not found any new ones. I looked extensively in the rule for Conway's Life (B3/S23) but, as Eppstein also noted, no self-replicating patterns were discovered.

I don't consider this last set of self-replicators to be examples of Fourier Life because they do not emerge spontaneously. But I include them here because the Fourier Transform method can detect them, and because they're interesting!

Self-Replicating Creatures

The self-replicating "creatures" come in three varieties (1D, x4 and sp), as indicated in parentheses after each Rule in the drop-down list above. This post describes some of the more interesting "creatures" discovered in the Fourier Life systems explored so far.

1D - Creatures which replicate along a one-dimensional line

• These are by far the most common type found
• They can appear as filled cells against an empty background as in Traffic (System B, Rule 15) or empty cells against a filled background as in Nighttime Traffic (System B, Rules 16)
• Sometimes the 1D creatures compete with others creatures, such as wick-stretchers in Qix! (System C, Rule 4), splitters in Butterflies vs Centipedes (System C, Rule 6) or four-fold replicators in Population Control (System C, Rule 9)
• The most interesting 1D replicators are ones where the line along which they replicate moves, either diagonally (System C, Rule 9) or horizontal/vertical (System C, Rule 10)

x4 - Creatures have 4-fold symmetry and create four new copies every replication period

• These are the most common 2-dimensional replicators
• The copies can sometimes be generated quite far away from the original, such as in Fourth of July (System B, Rule 1) where they are separated by twenty cells!
• The growth can be continuous as in Raindrops (System B, Rule 5) or can seemingly pause such as in Flowers in Bloom (System B, Rule 3)
• The replicator can be a continuously moving structure which spawns new copies as it moves outward, such as in Armadillos (System C, Rule 5)
• This type of replicator usually takes over the world quite easily since it makes four copies each replication period, e.g. Overcrowding (System C, Rule 8), but sometimes other replicators can compete with them, e.g. Population Control (System C, Rule 9).

sp - Creatures split into two (like 1D) but the new copies are rotated 90 degrees from the original so they eventually fill up the whole 2-dimensional world.

• These are the rarest type and, to me, the most interesting
• Amazingly enough, the very first self-replicating creature found was also the rarest type (System A, Rule 1)
• The splitting can appear very deliberate and defined such as in Manta Rays vs Gliders (System B, Rule 2) and Stingrays (System B, Rule 4) or more fluid such as in Shape Shifters (System C, Rule 1) and Rise of the Pheonix (System C, Rule 7). In these latter systems, it is necessary to step through the iterations to actually see how they split in two.
• Perhaps the most amazing system found so far is Bats on a Checkerboard (System B, Rule 8). These replicators live on a background of an oscillating checker board. The constant flashing is tough to watch so I added a checker-board mask. Once I did this, I realized that there were replicators in each of two different checker board backgrounds which appear light and dark with the mask. There is a semi-stable boundary between the two and keeps the two replicators separated. Over time, one area (either light or dark) eventually takes over the world although sometimes it can take more than a hundred thousand generations.
• Another variation of "checker-board life" discovered is Bricks on a Checkerboard (System B, Rule 9) but it is difficult to get it started so it's best to run it from Bats on a Checkerboard once the two regions are established.

The Solution: Fourier Transform

The key to finding emergent self-replicating creatures is to apply a Fourier Transform to the number of cells which are born, survive or die. For the original self-replicating rule set, here are the graphs:

The graphs above are slightly wavy with a period corresponding to the number of iterations the creature takes to self-replicate. The Fourier Transform is able to extract this information from the graphs, as shown below.

The Fourier transforms of the three traces reveal two important things. First, peaks or inflections appear at regular intervals, although all peaks are not present in all three traces. Second, the number of sections between the peaks is equal to the period of self-replication divided by two: there are 6 segments above and the period is 12.  For an odd-numbered self-replication period such as 7, the graph is separated into 3.5 segments with the half-segment on the right (higher values on x-axis).

Once the Fourier Transform is computed, it is simply a matter of finding the peaks located at regular intervals. One can go about this task in multiples ways, and the choices I describe below are only one possibility. However, the important result from the Fourier Transform is that periodic self-replication shows up as peaks at regular intervals, the location of which are determined by the number of iterations required to replicate.

Once the peaks were detected (I combined together the three graphs and then used a signal-to-noise ratio of >3.5 to detect peaks), the following parameters were calculated for each possible period of replication (I used 5 to 48):

• avg_hgt:  average peak height
• num_pks:  number of peaks detected
• frac_per:  fraction of peaks found for a given period out of the total number expected for that period
• frac_tot:  fraction of peaks in the given period out of the total number of peaks

Through a process of trial and error, the formula below was found to work well for finding self-replicating systems.

Selector = avg_hgt * 2^(num_pks/2) * frac_per^2 * frac_tot

The Selector is calculated for each possible period of replication (5-48) and the highest Selector value is saved for that run (usually 512 iterations).  Once again, other formulas will work as well.  And different formulas may work better for different rule systems. I have in fact tried many different formulas but I never ran enough trials to say which ones were better than others. The above is one of the simpler ones.

In a standard run, I randomly tested about 15,000 rules, calculating the Selector for each one and saving them in a database. I only ran each rule on a 100x100 grid for 512 iterations to see the diagnostic frequency peaks in the Fourier Transform. Then I analyzed the database, examining visually only the ones with Selectors above a certain value (usually Selector >100 using the formula above).

In other cases, I experimented with a genetic algorithm to find self-replicating systems. Each generation would consist of 30 rule codes, and I ran the experiment for 512 generations.  The process was fairly complicated, and at the end of the day it's not clear that it worked any better than just random chance for finding self-replicating systems. However, for the experiments that did find replicators, the genetic algorithm was able to find similar rule codes with similar replicators.

To see the emergent self-replicators I've discovered with this method, choose System B or C above and try the various Rules.

The Problem Defined

My goal was to find more self-replicating systems that emerge spontaneously from a random field of cells. I stumbled upon the first one (see System A, Rule 1 above) by testing lots of rules and looking at graphs of the number of live cells over time.  At first, I was just looking for more examples of interesting rules such as Conway's game of life (see green line below). However, when I found the first self-replicating system, I was much more interested in these because of the implications for the Origin of Life.

The problem is that the total number of rules is way too many to look through by hand (4,294,967,296 for the 2-rule system in which the original self-replicator was found). I needed some way to detect self-replicating systems, or to at least narrow down the number of rules to visually examine. One method would be to analyze the cells and look for repeating patterns. I imagined it would be difficult to write efficient code to do this. It would also be taxing on the cpu which would limit the number of rules that could be tested. Another approach would be to analyze the number of cells alive at each iteration, a number easily calculated as each iteration of the grid is generated. This second approach seemed promising based on a comparison of the graphs below.

The green line is the percentage of cells alive for each iteration of Conway's rules (B3/S23) starting from a random field of cells. The red line is the simple rule of B2/S3. The result of this rule set is just noise and the percentage of cells remains fairly constant.  The blue trace is the original self-replicating rule set (alternates between B3/S23 and B2/S56) where the creatures emerge from the random cells and replicate to take over the world.

The green and blue traces are similar but the blue, self-replicating trace has a unique feature:  there is a periodic nature to it as shown by the small vertical lines at the bottom.  The number of alive cells seems to rise and fall every 12 iterations.  If we look at the life cycle of the self-replicator below, we notice that the creature replicates itself every 12 iterations. The overall problem of detecting self-replicating systems was thus reduced to the problem of detecting periodic fluctuations in the population graphs.

Introduction to Fourier Life

Cellular Automata and the Origin of Life

Fourier Life deals with cellular automata, of which the most famous example is Conway's Game of Life.

After discovering the first system, I wanted to find more self-replicating systems which would spontaneously appear out of a random field of cells. The visual analogy to the first life forms spontaneously coming into existence from the primordial soup is striking. See my Implications post for more speculation on this analogy.

Others have discovered or invented self-replicating systems in cellular automata, a collection of which is demonstrated on this nice web site from the New England Complex Systems Institute. The work described on this web site is complimentary to this earlier work and differs in three important ways:

1. The self-replicating systems are emergent from a random population of cells--they were not designed.
2. The self-replicating creatures (for lack of a better term) appear in systems simpler than the previous ones (two- and three-state systems rather than six- to nine-state systems)
3. An algorithm using Fourier Transform was developed to find these emergent self-replicating systems

DISCLAIMER

I'm just a computer hobbyist, not a scientist in the field of artificial life (my day job is an organic chemist trying to discover new medicines).  As a result, I am not up-to-date on all the relevant research.  If you know of such research, please add a comment below.

What is Fourier Life?

Fourier Life is a system of cellular automata which spontaneously forms self-replicating structures. The picture above has the first system I found and shows 16 iterations of the system (each square with dots in it is a small portion of the cellular automata grid). Note that after 12 iterations, the original structure has replicated itself, although now each copy is rotated from the original. At each iteration (or generation), a filled cell either survives or dies and an empty cell can either remain empty or have a cell born into it. In the example above, the fate of each cell depends on how many neighbors (filled cells) it has surrounding it (up to 8).

If you click on the Run button (under the grid of cells at the top of the page) with System A and Rule 1 selected, you can see these structures appear out of a random field of cells, begin dividing in two, and then take over the entire cellular automata world.

This web site shows the more interesting self-replicating systems I've found and describes how I found them. The key to detecting self-replicating systems is to use a Fourier Transform on the population graphs.  As a result, I have named these systems Fourier Life.